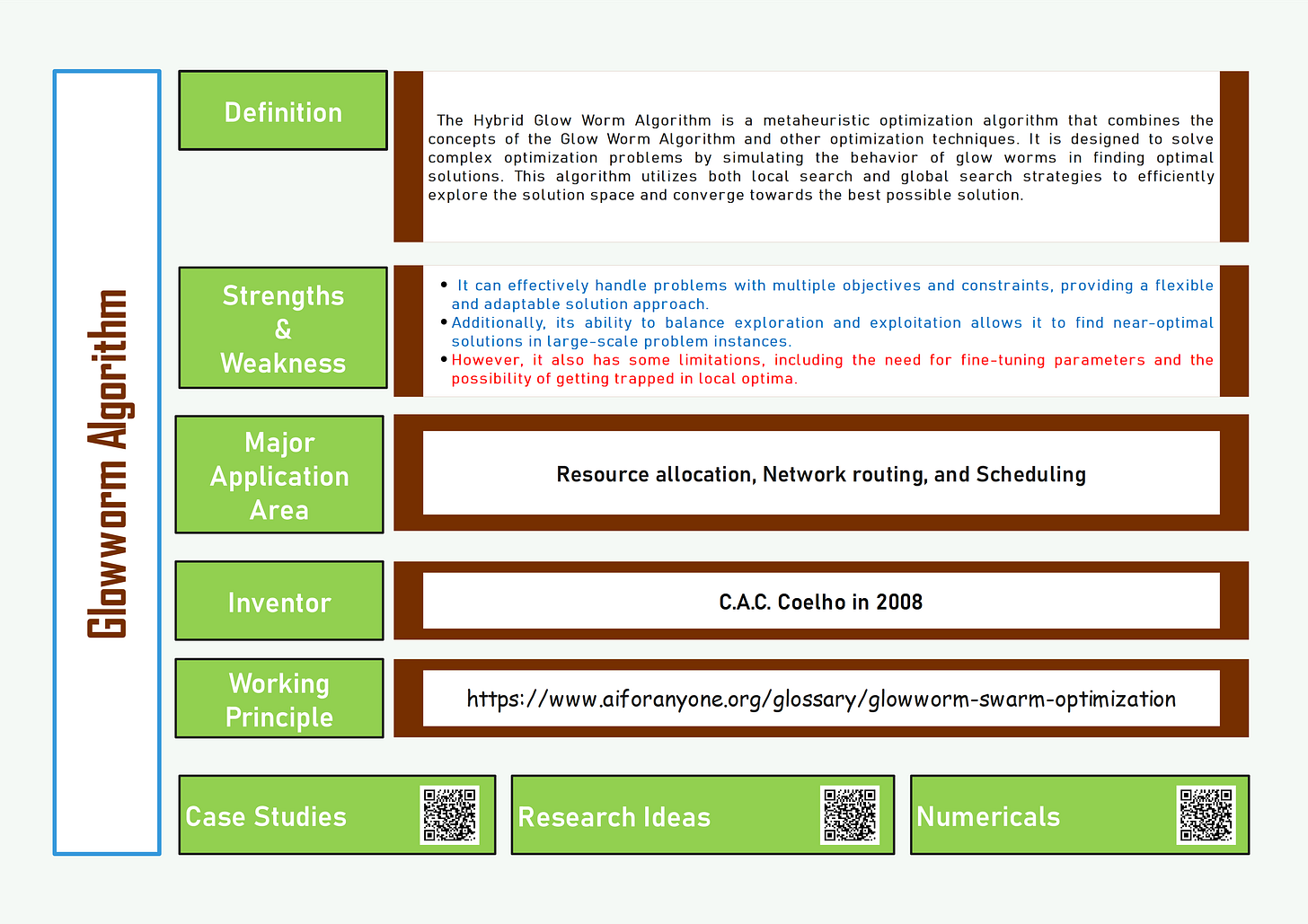
Glowworm Optimization Algorithm
The original Glow Worm Algorithm is a swarm intelligence-based optimization algorithm inspired by the behavior of glow worms in nature.
Click here to be eventful(Ad).
Case Studies/Example
Two-stage glowworm swarm optimisation for economical operation of hydropower station
Xiaoyu Wang, Kan Yang, Xianghua Zhou (2018)
This study proposes a two-stage glowworm swarm optimisation (GSO) algorithm for the economical operation of the inner plant of a hydropower station. Binary GSO and real-coded GSO (RCGSO) algorithms are applied with different types of encodings to solve the unit commitment sub-problem and the economic load distribution (ELD) sub-problem, respectively. Moreover, an improved dynamic patching mechanism is developed to avoid invalid calculations and enrich the diversity of the solutions. A luciferin transfer mechanism helps the algorithm escape the local optimum and a local research mechanism enhances the diversity of the solution space by selecting from among the derived solutions. The RCGSO algorithm uses a variable-step mechanism to avoid missing the optimal solution. In comparison with the genetic algorithm and particle swarm optimisation, the RCGSO is significantly robust and provides better solutions to ELD sub-problems. Numerical simulations exhibited the superiority of the two-stage GSO algorithm in terms of stably and quickly solving the economical operation problem of hydropower stations.
Demand Estimation of Water Resources based on Coupling Algorithm
Jiangjiang Zhang; Zhuanghua Zhu; Yu Chang; Di Wu; Lei Du; Zhihua Cui et.al. (2019)
Demand estimation of water resources is an important basic content in the process of urban water resources planning. To predict water resource demand accurately, a coupling algorithm based on bacterial foraging optimization algorithm (BFOA) and glowworm swarm optimization (GSO) is employed to estimate the demand of water resources in this paper. The historical data (2003-2015) is divided into two parts for convenience in the simulation experiments, one (2003-2012) is trained to gain the weighting factors of the estimation and the other (2013-2015) is used for predicting and evaluating water resources. In addition, the simulation results show that the coupling algorithm achieves a higher accuracy compare with BFOA and GSO on prediction.
Evolutionary algorithms, swarm intelligence methods, and their applications in water resources engineering: a state-of-the-art review
M. Janga Reddy; D. Nagesh Kumar (2020)
During the last three decades, the water resources engineering field has received a tremendous increase in the development and use of meta-heuristic algorithms like evolutionary algorithms (EA) and swarm intelligence (SI) algorithms for solving various kinds of optimization problems. The efficient design and operation of water resource systems is a challenging task and requires solutions through optimization. Further, real-life water resource management problems may involve several complexities like nonconvex, nonlinear and discontinuous functions, discrete variables, a large number of equality and inequality constraints, and often associated with multi-modal solutions. The objective function is not known analytically, and the conventional methods may face difficulties in finding optimal solutions. The issues lead to the development of various types of heuristic and meta-heuristic algorithms, which proved to be flexible and potential tools for solving several complex water resources problems. This paper provides a review of state-of-the-art methods and their use in planning and management of hydrological and water resources systems. It includes a brief overview of EAs (genetic algorithms, differential evolution, evolutionary strategies, etc.) and SI algorithms (particle swarm optimization, ant colony optimization, etc.), and applications in the areas of water distribution networks, water supply, and wastewater systems, reservoir operation and irrigation systems, watershed management, parameter estimation of hydrological models, urban drainage and sewer networks, and groundwater systems monitoring network design and groundwater remediation. This paper also provides insights, challenges, and need for algorithmic improvements and opportunities for future applications in the water resources field, in the face of rising problem complexities and uncertainties.
Economic load dispatch of renewable energy-based power systems with high penetration of large-scale hydropower station based on multi-agent glowworm swarm optimization
Xiaoyu Wang, Kan Yang (2019)
In this study, we propose a multi-agent glowworm swarm optimization (MAGSO) algorithm for the economic load dispatch (ELD) problem of a large-scale hydropower station. The MAGSO integrates the idea of the evolution of glowworm swarm optimization (GSO) and the interindividual cooperation of multi-agent system (MAS). In this structure, each glowworm of the GSO is treated as an agent cooperating in the MAS before entering the evolutionary process. The proposed mechanisms enable the algorithm to escape from local extremum, capture the optimal solution and expand the diversity of solution space. The test results of four benchmark functions verify the advantages of the algorithm in global search, convergence speed and avoiding prematurity. In comparison of two case studies with the real genetic algorithm (RGA), the evolution programming (EP), the particle swarm optimization (PSO), the ant colony optimization (ACO), and the standard glowworm swarm optimization (GSO), the MAGSO provides significantly robust solutions of ELD problem of a large-scale hydropower station.
Demand estimation of water resources based on algorithm comparison
Junyan Wang, Jiangjiang Zhang, Xingjuan Cai and Yanyan Ma (2019)
Water is the source of life and the correct assessment of water resources is an important pre-requisite for the rational utilisation of water resources. In this paper, water resources are evaluated and predicted by three different algorithms, including Bat Algorithm (BA), Particle Swarm Optimisation (PSO) and Pigeon-Inspired Optimisation (PIO). Comparing the errors of water resources assessed for the three algorithms, we select an algorithm of the minimum error to predict the future water demand. In the experiments, firstly, the water data from 2003 to 2012 are used to find the optimal weights of the models. Then, the weight factor is combined with the given model to gain the error between predicted value and the remaining data (2013-2015). Finally, the simulation results show that PIO algorithm has a better performance compared with the BA and PSO algorithms.
Research Ideas
The Glowworm Optimization Algorithm can be applied to find a better solution for the following problems of water research due to its fast convergence rate and ability to avoid local minima:
Micro-Irrigation planning
Multi-Reservoir Operation Optimization for Silt Minimization
Crop water allocation for maximization of agricultural productivity under minimum cost
Water conveyance/shortest route-finding problems
Pressure and Cost Minimization of stormwater and sewage transportation networks
Parameter estimation of hydrological models
Reservoir Routing Problems
Minimization of the Number of Groundwater Monitoring Wells
Minimization of total piping and excavation cost for sewer disposition
Minimization of wastewater dumping and releasing cost
Numericals
A rectangular pen with a divider down the middle is to be built using 120 m of fencing. Find the dimensions that should be used in order to maximize the area of the enclosed region.
A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides Given 100ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?
An open-top box is to be made from a 24in by 36in piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?
An island is 2 mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 6 mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of 8 mph and swims at a rate of 3 mph. How far should the visitor run before swimming to minimize the time it takes to reach the island?
A rectangular box with a square base, an open top, and a volume of 216 cubic inches is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?
Participate in the Test and Earn Certificates by qualifying. Enroll for the Baipatra Course on Glowworm Optimization Algorithm (Part of the course: “ Introduction to Optimization Techniques”)
You may also like :
HydroGeek may receive affiliate commissions from some of the links given above. All the commissions will be deposited to NGOs and NPOs after the deduction of the honorariums, maintenance, and taxes for running this site.
Follow me on Gumroad / Twitter / Listly / Youtube
HydroGeek is a reader-supported publication. To support my work, consider becoming a paid subscriber or gift a subscription to someone you know will be interested in this newsletter.
Thanks for reading the entire article as a Thank You Gift for reading the entire article I will increase the discount on the annual plan by 20%. Click on the button below to claim this offer :
Video Walk Through on How to apply GWO in optimization technique problems
(Workable spreadsheet included)