If you're enjoying the articles in this newsletter, we’d be grateful for your support. You can contribute by making a donation, submitting your own articles, joining us as a paid member(click here to pay in INR), or sponsoring us(Contact us for more details. Email at contact@baipatra.ws). Your support, in any form, is vital to helping us sustain and grow. Thank you!
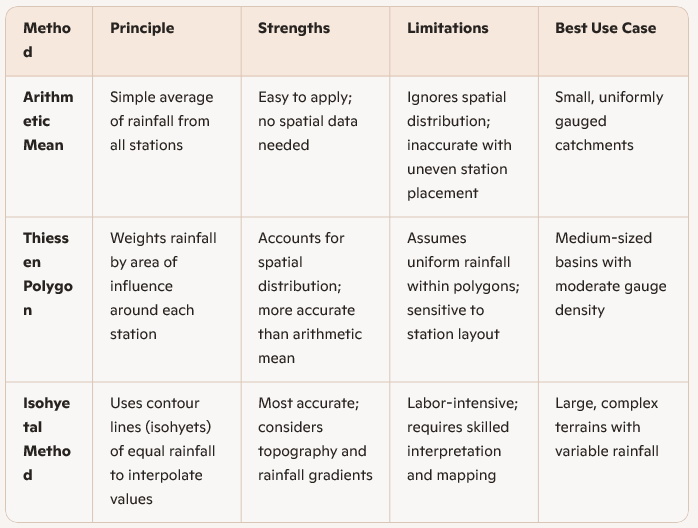
The Thiessen Polygon Method is a widely used technique for estimating mean precipitation over a catchment area by assigning weighted values to rainfall data from multiple stations. Developed by Alfred H. Thiessen in 1911, this method involves dividing the region into polygons, each centered around a rain gauge. These polygons are constructed by connecting adjacent stations with straight lines and then drawing perpendicular bisectors to form boundaries. The assumption is that rainfall within each polygon is uniform and best represented by the gauge at its center. The mean precipitation is calculated by multiplying the rainfall recorded at each station by the area of its corresponding polygon, summing these products, and dividing by the total area of the catchment(Source 1 and 2).
This method is particularly useful in hydrological studies where spatial variability of rainfall needs to be accounted for, especially in regions with uneven distribution of rain gauges. Compared to the arithmetic mean method, which gives equal weight to all stations, the Thiessen approach provides a more realistic estimate by considering the spatial influence of each gauge. However, it assumes uniform rainfall within each polygon and may not be suitable for areas with complex terrain or highly variable precipitation patterns. Despite its limitations, the Thiessen Polygon Method remains a practical and effective tool for estimating areal rainfall in many engineering and environmental applications(Source 2 and 3).
Comparison between the different methods of Mean Precipitation Estimation
The Thiessen Polygon Method strikes a balance between simplicity and spatial realism. It’s more refined than the arithmetic mean, yet less demanding than the isohyetal approach. For catchments between 500–5000 km², especially where gauges are unevenly distributed but terrain isn’t too complex, Thiessen offers a practical and reasonably accurate solution.
Subscribe to my YouTube Channel for the full video or become a paid member of HydroGeek Newsletters